Estatística Descritiva

Como classificar variáveis, construir tabelas e desenhar gráficos.

Variáveis

Características de interesse da amostra ou população.

  • Qualitativa: aquela que define uma qualidade sem valor numérico.
    • Nominal: que não tem nenhuma relação de ordem.
      • Exemplos: nome, cor, doente/sadio, esportista/sedentário.
    • Ordinal: que tem alguma relação de ordem intrínseca.
      • Exemplos: grau de escolaridade.
  • Quantitativa: aquela que define uma qualidade com valor numérico.
    • Discreta: assumem valores equivalentes aos números inteiros.
      • Exemplos: números de filhos, número de cigarros fumados por dia, número de carros.
    • Contínua: assumem valores equivalentes os números reais.
      • Exemplos: peso, altura, pressão arterial.

Dados ou Informações

  • Dados Brutos: dados populacionais obtidos sem nenhum tratamento.
  • Rol: dados organizados de forma crescente ou decrescente.
  • Tabela de Frequência: cada linha indica quantas vezes cada valor é observado.

Agrupamento de Valores

  • Amplitude de uma variável: diferença entre o maior e menor valor da variável.
  • Classe: um grupo de valores.
  • Limites de uma Classe: maior e menor valor da classe.
  • Regra de Sturges: se a população tem $n$ elementos, então o número de classes $k$ desejado em uma tabela é $$k = 1 + 3.3 \log_{10} (n).$$

Nomenclatura

Em um contexto de uma tabela de distribuição de frequência e população com $n$ elementos e com rol de valores observados $x_1 < x_2 < x_3 < \cdots < x_k$:

  • Frequência simples absoluta ($n_i$): número de observações de um determinado valor.
  • Frequência simples relativa ($f_i$): proporção de observações em relação ao todo ($n_i/n$).
  • Frequência acumulada absoluta ($N_i$): número total de observações abaixo de um certo valor ($\sum_{j = 1}^i n_i$).
  • Frequência acumulada relativa ($F_i$): proporção de observações abaixo de um certo valor em relação ao todo ($\sum_{j = 1}^i f_i$).

Exemplo Prático

Aqui você pode encontrar o arquivo original para o exemplo abaixo.

No exemplo temos uma tabela fictícia com o desempenho de algumas pessoas em testes.

Na tabela, existem as seguintes variáveis que podem ser classificadas como:

  • gênero/sexo: qualitativa nominal.
  • raça/etnia: qualitativa nominal.
  • nível escolar dos pais: qualitativa ordinal.
  • tipo de almoço: qualitativa nominal.
  • curso preparatório para o teste: qualitativa nominal.
  • resultado no teste de matemática: quantitativa discreta.
  • resultado no teste de leitura: quantitativa discreta.
  • resultado no teste de escrita: quantitativa discreta.

Abaixo podemos ver algumas tabelas de distribuição de frequência para essas variáveis.

Distribuição de frequência do gênero/sexo:

gênero/sexo $n_i$ $f_i$
masculino 518 51.80%
feminino 482 48.20%
TOTAL 1000 100.00%

Distribuição de frequência da raça/etnia:

raça/etnia $n_i$ $f_i$
grupo A 89 8.90%
grupo B 190 19.00%
grupo C 319 31.90%
grupo D 262 26.20%
grupo E 140 14.00%
TOTAL 1000 100.00%

Distribuição de frequência do nível escolar dos pais:

nível escolar paterno $n_i$ $f_i$
ensino fundamental incompleto 179 17.90%
ensino fundamental completo 196 19.60%
ensino técnico 222 22.20%
superior incompleto 226 22.60%
superior completo 118 11.80%
pós-graduação 59 5.90%
TOTAL 1000 100.00%

Distribuição de frequência do tipo de almoço:

almoço $n_i$ $f_i$
reduzido 355 35.50%
normal 645 64.50%
TOTAL 1000 100.00%

Distribuição de frequência do curso preparatório:

curso $n_i$ $f_i$
não fez 358 35.80%
completou 642 64.20%
TOTAL 1000 100.00%

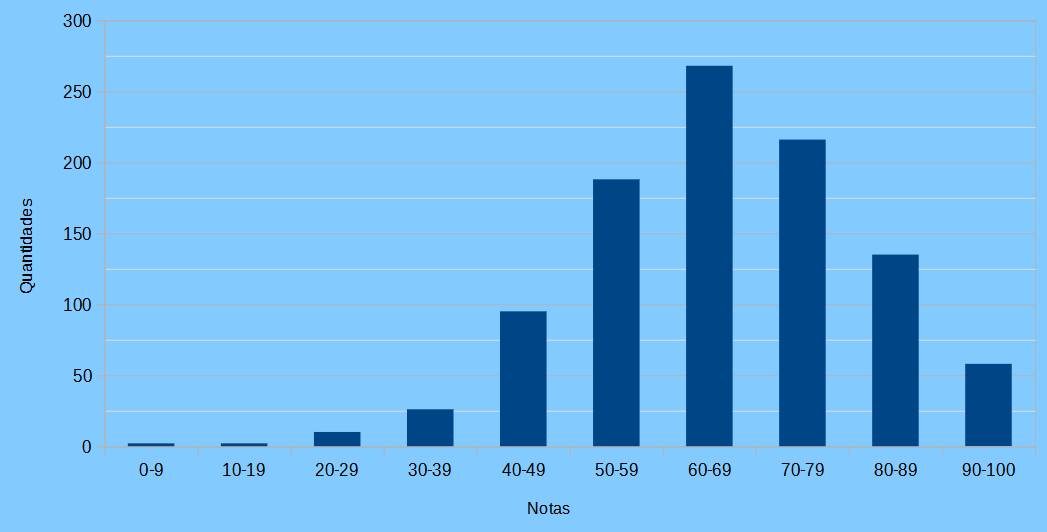
Distribuição de frequência do resultado do teste de matemática:

Aqui temos um problema. Como são muitas notas, teremos que agrupar elas em classes senão a tabela de distribuição de frequência teria mais ou menos umas 100 linhas. Escolhendo 10 classes ficamos com:

matemática $n_i$ $f_i$ $N_i$ $F_i$
0-9 2 0.20% 2 0.20%
10-19 2 0.20% 4 0.40%
20-29 10 1.00% 14 1.40%
30-39 26 2.60% 40 4.00%
40-49 95 9.50% 135 13.50%
50-59 188 18.80% 323 32.30%
60-69 268 26.80% 591 59.10%
70-79 216 21.60% 807 80.70%
80-89 135 13.50% 942 94.20%
90-100 58 5.80% 1000 100.00%
Total 1000 100.00% 1000 100.00%

Distribuição de frequência em classes do resultado do teste de leitura:

leitura $n_i$ $f_i$ $N_i$ $F_i$
17-26 5 0.50% 5 0.50%
27-36 10 1.00% 15 1.50%
37-46 51 5.10% 66 6.60%
47-56 126 12.60% 192 19.20%
57-66 227 22.70% 419 41.90%
67-76 262 26.20% 681 68.10%
77-86 206 20.60% 887 88.70%
87-96 88 8.80% 975 97.50%
97-106 25 2.50% 1000 100.00%
Total 1000 100.00% 1000 100.00%

Distribuição de frequência em classes do resultado do teste de escrita:

escrita $n_i$ $f_i$ $N_i$ $F_i$
10-19 3 0.30% 3 0.30%
20-29 6 0.60% 9 0.90%
30-39 23 2.30% 32 3.20%
40-49 82 8.20% 114 11.40%
50-59 167 16.70% 281 28.10%
60-69 230 23.00% 511 51.10%
70-79 254 25.40% 765 76.50%
80-89 157 15.70% 922 92.20%
90-100 78 7.80% 1000 100.00%
Total 1000 100.00% 1000 100.00%

Gráficos

São desenhos que visam transmitir informações.

Histogramas

Gráfico em barras em que o eixo horizontal representa as classes da variável analisada e o eixo vertical a quantidade de observações.

Figura de Histograma
Histograma da notas de matemática agrupadas em classes

DotPlot (gráfico de pontos)

Gráfico que mostra a distribuição de frequência de variáveis quantitativas por meio de pontos.

Figura de DotPlot

StemPlot (ramos-e-folhas)

Gráfico que mostra a distribuição de frequência de variáveis quantitativas por meio de categorias.

Figura de StemPlot

Time Series (séries temporais)

Gráfico que mostra a evolução de uma variável ao longo do tempo.

Figura de Série Temporal

Gráfico de Pareto

Um histograma em que as classes da variável estão dispostas em ordem decrescente de observações.

Gráfico de Pareto

Gráfico em pizza

Gráfico em formato circular em que o tamanho de um arco reflete a quantidade de observações relativa.

Gráfico em Pizza

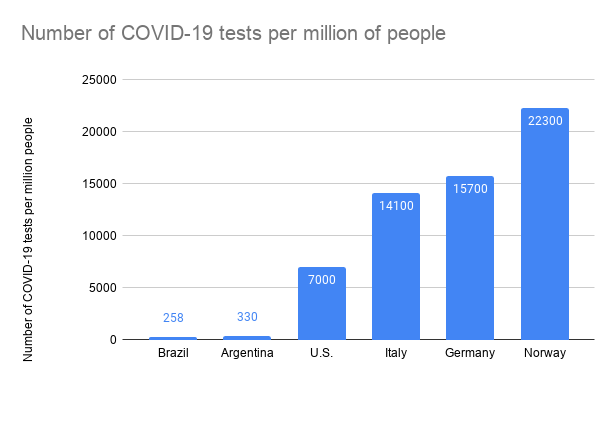
Mal uso de Gráficos

Usados fora de escala, ou com escala quebrada, podem levar à uma interpretação errada dos dados.

Exemplos

Os exemplos abaixo podem ser encontrados aqui.

Testes para COVID-19 na Argentina

Testes de Covid na Argentina
Gráfico da C5N sobre testes de COVID na Argentina
Gráfico Corrigido
Gráfico Correto

A Russia achatou a curva

Gráfico Corrigido
Gráfico Russo
Gráfico Corrigido
Gráfico Correto

Exemplos de Análises Estatísticas

Fontes de Bancos de Dados

Um bom lugar para encontrar bancos de dados públicos é o site Kaggle.

Exercício Resolvido

Vamos analisar a Qualidade da Água Potável disponível no Kaggle.

Como o arquivo no Kaggle tem alguns problemas para importar os dados para análise, eu limpei esse arquivo e coloquei uma versão aqui: Qualidade da Água para importação.

O primeiro passo é abrir um arquivo com um editor de sua preferência e importar os dados csv. As configurações do arquivo aqui do site são:

  • delimitador: , (vírgula).
  • formato/codificação: utf-8.
  • separador de texto: ” (aspas duplas).

Um arquivo com os valores já importados no formato do open office também pode ser encontrado aqui.

Parte 1: Classificar os tipos de variáveis encontradas no banco de dados.

Variaveis encontradas:

  • Sample Date/Data da amostra: Qualitativa ordinal.
  • Sample Time/Horário da amostra: Qualitativa ordinal.
  • Sample Site/Local da Amostra: Qualitativa nominal.
  • Sample class/Classe da Amostra: Qualitativa nominal.
  • Location/Localização:Qualitativa nominal.
  • Residual Free Chlorine (mg/L)/Cloro residual: Quantitativa contínua.
  • Turbidity (NTU)/Turvação: Quantitativa contínua.
  • Fluoride (mg/L)/Fluoreto: Quantitativa contínua.
  • Coliform (Quanti-Tray) (MPN /100mL)/Coliformes: Quantitativa contínua.
  • E.coli(Quanti-Tray) (MPN/100mL): Quantitativa contínua.

Parte 2: Tabelas de Distribuição de Frequência.

Fazer as tabelas de distribuição de frequência de algumas das variáveis agrupando os valores quando fizer sentido.

Parte 3: Histogramas.

Construir os histogramas dessas mesmas variáveis.

Resultado Final

Um arquivo exemplo com tabelas e histogramas pode ser encontrado aqui.

Atualizado em: